Page 493 - Ebook HTKH 2024

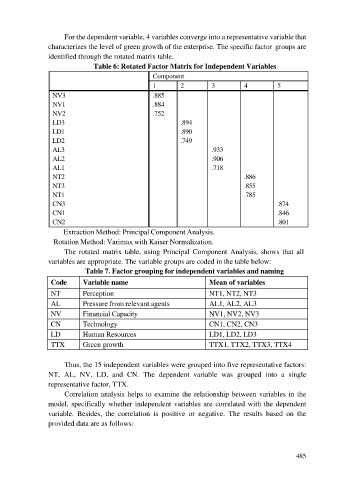
For the dependent variable, 4 variables converge into a representative variable that
characterizes the level of green growth of the enterprise. The specific factor groups are

identified through the rotated matrix table.
Table 6: Rotated Factor Matrix for Independent Variables
Component
1 2 3 4 5
NV3 .885
NV1 .884
NV2 .752
LD3 .894
LD1 .890
LD2 .749
AL3 .933
AL2 .906
AL1 .718
NT2 .886
NT3 .855
NT1 .785
CN3 .874
CN1 .846
CN2 .801
Extraction Method: Principal Component Analysis.
Rotation Method: Varimax with Kaiser Normalization.
The rotated matrix table, using Principal Component Analysis, shows that all
variables are appropriate. The variable groups are coded in the table below:
Table 7. Factor grouping for independent variables and naming

Code Variable name Mean of variables
NT Perception NT1, NT2, NT3

AL Pressure from relevant agents AL1, AL2, AL3
NV Financial Capacity NV1, NV2, NV3
CN Technology CN1, CN2, CN3
LD Human Resources LD1, LD2, LD3

TTX Green growth TTX1, TTX2, TTX3, TTX4

Thus, the 15 independent variables were grouped into five representative factors:
NT, AL, NV, LD, and CN. The dependent variable was grouped into a single
representative factor, TTX.

Correlation analysis helps to examine the relationship between variables in the
model, specifically whether independent variables are correlated with the dependent
variable. Besides, the correlation is positive or negative. The results based on the
provided data are as follows:

485